- Определение фокусных расстояний линз
- Описание экспериментальной установки
- Самые интересные ролики на Youtube
- Небольшой экскурс в оптическую геометрию
- Фокусное расстояние собирающей линзы
- Фокус рассеивающей линзы
- Что представляет собой фотоаппарат
- Конспект урока «Линзы. Фокусное расстояние линзы.Построение изображений в линзах»
Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими.
Определение фокусных расстояний линз
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ СОБИРАЮЩИХ И
Цель работы : научиться определять фокусные расстояния собирающих и рассеивающих линз.
Приборы и принадлежности : набор линз; осветитель; экран.
Оптические линзы представляют собой тела из прозрачного вещества (стёкла, прозрачные кристаллы, пластмассы и т. д.), ограниченные двумя сферическими поверхностями, вершины которых лежат на одной оси, называемой оптической осью (рис.1).
Рис.1. Различные типы собирающих и рассеивающих линз
Для тонких линз имеет место соотношение:
где b – расстояние от линзы до изображения; а – расстояние от линзы до предмета; f – фокусное расстояние линзы. Знаки расстояний, входящих в формулу (1), можно определять по простому правилу: если расстояние отсчитывается от линзы по ходу луча, то ему приписывают знак «+», в противном случае — « — ».
На рисунке 1 показаны различные типы собирающих и рассеивающих линз: а) двояковыпуклая; б) плосковыпуклая; в) выпукло-вогнутая; г) двояковогнутая; д) плосковогнутая; е) вогнуто-выпуклая. Около соответствующих рисунков показаны характеристики линз: радиусы кривизны и фокусы. К собирающим линзам относят типы а, б, в, к рассеивающим — г, д, е. У первых середина линзы толще, чем края, у вторых края толще, чем середина.
Описание экспериментальной установки
Установка для измерения фокусных расстояний собирающих и рассеивающих линз представлена на рис. 2.
Рис. 2. Установка для измерения фокусных расстояний собирающих и рассеивающих линз
Установка состоит из источника света 1 с наклеенной на нем стрелкой, играющей роль предмета. Источник света 1 установлен на основании 2. Экран 6, на котором получается изображение, установлен на основании 4. Основания 2 и 4 скрепляются между собой при помощи стержней, по которым могут перемещаться одна или несколько исследуемых линз 3. Вертикальность расположения установки можно регулировать при помощи ножек 7.Установка снабжена метровой шкалой, позволяющей определить положение линз в каждом из опытов. Каждая из линз может быть независимо удалена из оптического тракта.
В случае линз вогнутых их фокусное расстояние изображения f’ — это величина отрицательная, поэтому оба слагаемых в правой части гауссовой формулы будут иметь знак минус, их править не нужно. Этот факт говорит о том, что где бы ни располагался предмет перед рассеивающим оптическим стеклом, его изображение будет всегда мнимым.
Самые интересные ролики на Youtube
Недавно мне потребовалось срочно заказать бифокальные очки для работы, а для этого потребовался рецепт. Идти к врачу было хлопотно и дорого. Да и измерения, сделанные впопыхах, вовсе не гарантировали идеальный результат, в чём я уже не раз убеждался.
По сути ведь приходится платить за то, что у врача есть набор линз и линейка. В кабинетах же, оснащённых современным оборудованием, тарифы и вовсе какие-то заоблачные, хотя результатом является всё тот же небольшой клочок бумаги.

Но, ведь некоторый набор линз и линейка обычно имеются у каждого очкарика с многолетним стажем, особенно, если вдобавок он ещё и самодельщик.

В спокойной, домашней обстановке, подобрать линзы несложно, но как определить оптическую силу линз, чтобы можно было заполнить рецепт?

Конечно, можно было бы напрячься и узнать местонахождение мастерской, где врезают линзы в оправы, а потом попытаться за некоторую плату измерить все свои линзы на линзметре (диоптриметре).
Но, я всё же решил сделать всё своими руками, поэтому первым делом отправился в Интернет, чтобы найти инструкцию по замеру этого параметра в домашних условиях.

Но, как часто бывает, советы умозрительных специалистов из сети оказались полностью неработоспособными. Так что, пришлось разрабатывать собственную технологию подобных измерений.
Результатом этих трудов стала данная статья и новые бифокальные очки, которые совершенно не утомляют ни глаза, ни голову. Кроме этого, я узнал почему некоторые очки не прижились у меня на носу.
А теперь обо всём этом подробнее.
Небольшой экскурс в оптическую геометрию
Вспомним школьный курс оптической геометрии, чтобы понять, для чего нам придётся измерять фокусное расстояние линзы.
Всё дело в том, что оптическая сила линзы – величина, обратно пропорциональная фокусному расстоянию.
D – оптическая сила в диоптриях,
F – фокусное расстояние в метрах.
Например, линза с оптической силой в +3 диоптрии, будет иметь следующее фокусное расстояние:
F = 1/D = 1/3 ≈ 0,33(метра)
Помните, как в детстве мы выжигали дырочки в бумаге с помощью папиной лупы?
Формула, описывающая процесс этой забавы выглядит так:
D = 1/L + 1/Lsun = 1/L + 1/∞ ≈ 1/L
D – оптическая сила в диоптриях
L – расстояние от оптического центра линзы до бумаги
Lsun – расстояние от Солнца до оптического центра линзы (можно принять равным бесконечности)
Но, Солнце слишком яркий и слишком громоздкий источник света, который, к тому же, может быть недоступен довольно длительное время.
Хотя, я и попробовал использовать наше светило для этого замера, точность измерений оказалось недостаточной. А вот использование точечного источника света позволило получить вполне приемлемые результаты.
Для упрощения измерений, скопируйте следующий текст в окно программы «Калькулятор-блокнот» и внесите туда же значения переменных L, S и С. Затем нажмите на Enter.
Фокусное расстояние собирающей линзы
Если рассмотреть ход лучей через собирающую линзу, то можно понять, почему она называется так. Лучи, проходящие через собирающую линзу, отклоняются в сторону главной оптической оси. А значит, параллельный пучок лучей после линзы пересечётся в некоторой точке, лежащей на этой прямой.
Точка, в которую собираются лучи, параллельные главной оптической оси после прохождения сквозь линзу, называется фокусом. У линзы имеется два фокуса, расположенные по разным сторонам от оптического центра. Расстояние от оптического центра линзы до её фокуса называется фокусным расстоянием линзы. Плоскость, проходящая через фокус и перпендикулярная главной оптической оси, называется фокальной плоскостью.
Для нахождения фокусного расстояния собирающей линзы строят схему прохождения лучей, основываясь на радиусах кривизны поверхностей $R_1$ и $R_2$, а также на коэффициенте преломления линзы $n$. Используя законы геометрической оптики, можно получить формулу фокусного расстояния собирающей линзы:
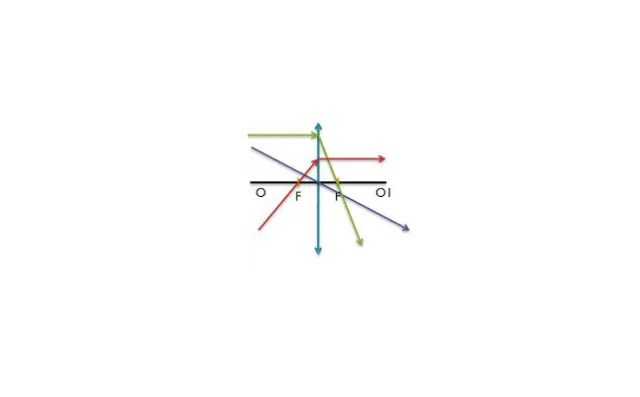
Рис. 2. Ход лучей в собирающей линзе.
Фокус рассеивающей линзы
Казалось бы, у рассеивающей линзы фокуса нет. В самом деле, если лучи, прошедшие через неё, отклоняются в сторону от главной оптической оси, где точка, в которой они соберутся?
Однако если мысленно продолжить линии хода лучей, то будет видно, что параллельные лучи, прошедшие сквозь рассеивающую линзу, далее идут так, будто они вышли из точки, лежащей на главной оптической оси, находящейся перед линзой.
Это и есть фокус рассеивающей линзы. Поскольку реально лучи не выходили из этой точки, фокус называется мнимым. И, раз фокус находится не за, а перед линзой, фокусное расстояние рассеивающей линзы получается отрицательным.
Все построения и принципы для рассеивающей линзы сохраняются. В ней также два фокуса, расположенные по разные стороны от линзы, и формула фокусного расстояния остаётся прежней, но, чтобы получить в оптическом центре меньшую толщину линзы, кривизна поверхностей $R_1$ и $R_2$ должна быть отрицательной. В результате и фокусное расстояние рассеивающей линзы также получается отрицательным.
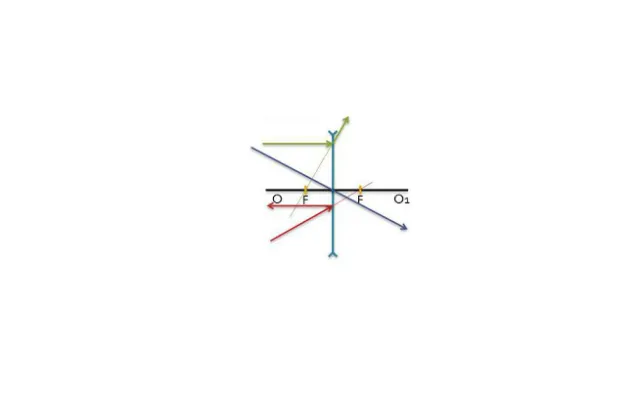
Рис. 3. Ход лучей в рассеивающей линзе.
В настоящее время часто используемыми оптическими системами являются линзы. Они применяются при изготовлении очков, фотоаппаратов, видеокамер и других приборов для оптики. Формула тонкой линзы в физике является основным математическим инструментом для полного описания этого объекта.
Что представляет собой фотоаппарат
Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора.
Особенность работы фотоаппарата в том, что на плоской фотопленке получаются довольно резкие изображения предметов, которые находятся на различных расстояниях. Резкость меняется вследствие перемещения объектива относительно фотопленки. Изображения точек, которые не лежат в плоскости резкого наведения, выходят на снимках размытыми в виде рассеянных кружков. Размер d данных кружков можно уменьшить методом диафрагмирования объектива, то есть уменьшения относительного отверстия a F , как показано на рисунке 3 . 3 . 5 . Это в результате увеличивает глубину резкости.

Рисунок 3 . 3 . 5 . Фотоаппарат.
С помощью проекционного аппарата удается снять масштабные изображения. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D ) на удаленном экране Э (рисунок 3 . 3 . 6 ). Система линз K (конденсор) используется для концентрации света источника S на диапозитиве. На экране воссоздается увеличенное перевернутое изображение. Масштаб проекционного устройства можно изменять, приближая или отдаляя экран и одновременно изменяя расстояние между диапозитивом D и объективом O .
8. В каких случаях получаются действительные изображения, а в каких -мнимые? Чем действительное изображение отличается от мнимого? При каких условиях изображение переносится в бесконечность?
Конспект урока «Линзы. Фокусное расстояние линзы.Построение изображений в линзах»
В данной теме будет рассмотрено решение задач на построение изображений в линзе.
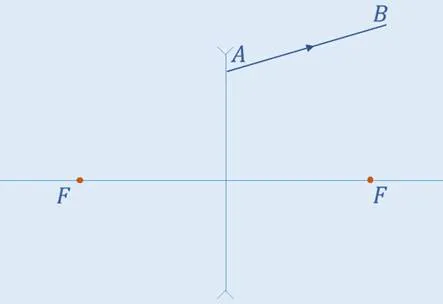
Задача 1. На рисунке изображен предмет АВ и собирающая линза. Постройте изображение предмета если он находится а) за двойным фокусом б) между фокусом и двойным фокусом.
Изобразим на чертеже собирающую линзу, её главную оптическую ось, фокусы и двойные фокусы.
Двойной фокус – это точка, находящаяся на оптической оси на расстоянии от оптического центра, вдвое большем, чем фокусное расстояние. Изобразим предмет АВ, находящийся за двойным фокусом.
Точка А находится на оптической оси линзы, поэтому её изображение тоже будет находится на оптической оси. Чтобы получить изображение точки В, понадобится два луча. Один направим параллельно оптической оси, а второй – через оптический центр. Лучи, проходящие через оптический центр, не преломляются, поэтому легко можем продолжить последний луч. Луч, параллельный оптической оси преломляется, и после преломления проходит через фокус линзы. На пересечении этих лучей и формируется изображение точки В, которое обозначим как B’. Точка A’ будет находится на главной оптической оси.

Во втором случаи поступаем таким же образом используя два луча.
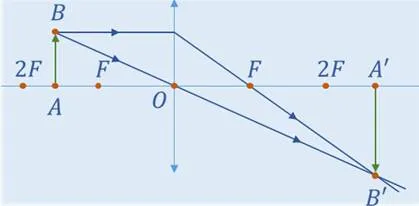
Таким образом, получено действительное и перевёрнутое изображение. Только в этот раз оно является увеличенным и находится за двойным фокусом.
Задача 2. На рисунке указан источник света и его изображение в линзе. Также на рисунке указана главная оптическая ось линзы. На основании этих данных, найдите положение оптического центра линзы, её фокусов, а также определите тип линзы.
В первую очередь, проведём прямую через источник света и его изображение (она называется побочной оптической осью). Точка пересечения этой прямой с главной оптической осью является оптическим центром линзы.
Обозначим на нашем чертеже линзу. От источника света направим луч на линзу параллельно главной оптической оси. Известно, что луч преломляясь идёт через фокус и через изображение (или же, через изображение идёт продолжение луча). Проведём пунктирную прямую через точку, в которой луч падает на линзу и через изображение источника света. Точка, в которой данная прямая пересекает главную оптическую ось и будет являться фокусом линзы.
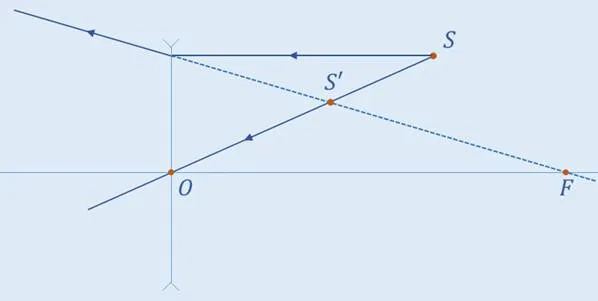
Теперь, с уверенностью можно сказать, что прямая, которую построили является продолжением преломлённого луча. По характеру преломления луча или, исходя из того, что изображение мнимое и находится ближе фокуса, можно заключить, что линза является рассеивающей.
Задача 3. На рисунке изображен луч АВ, прошедший через рассевающую линзу. Также, на рисунке указаны положения фокусов линзы. Постройте ход падающего луча.